Gnillehcs' Model of Integration
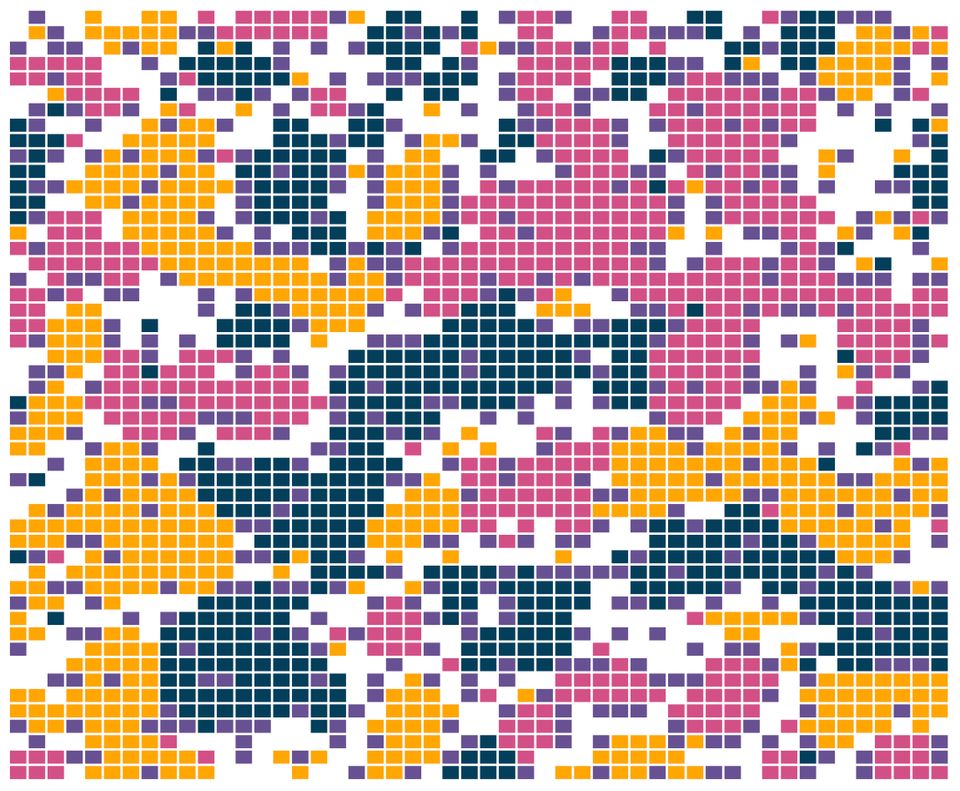
In the 1960s, Thomas Schelling developed a computational model that demonstrated how even a mild preference for neighbours of the same race or ethnicity can lead to high levels of segregation in a community. The original model assumed that all households preferred to live near others of the same kind. In this article we explore what happens when some households seek diversity instead - a variation on the original model I'm calling "Gnillehcs' Model of Integration".
To do this, I built a Streamlit application. We won't cover the specifics of how Schelling's model of segregation works here, so if you're not familiar with it, I recommend checking out this article which I used as the foundation of my project.
My implementation provides some additional features that are necessary for this analysis:
- It allows for more that two types of household to be specified.
- It enables diversity-seeking behaviour amongst households. Whereas similarity preference thresholds in the original model are configured as positive percentages, this model also accepts negative percentages. A negative percentage specifies the minimum percentage of neighbours that a household wants to be of a different type to them.
- It enables dynamic group thresholds that change linearly between two configured values throughout the simulation (more on this later).
The Streamlit application used for the simulations discussed below can be found here.
Schelling's Model of Segregation
The original Schelling model of segregation is an agent-based model that starts with a grid of cells, each representing a household. Each household is occupied by a person of a specified type. Depending on their type, each person has a preference for the minimum percentage of people in their neighbourhood that they want to be of the same type as them. For example, person of type A might prefer for at least 50% of their neighbours to also be type A. This is illustrated in Simulation 1.
We see that from a random starting point, the two groups rapidly segregate themselves into homogeneous regions.
Adding a Diversity-Seeking Group
In our modified version of the model, some households have a preference for diversity instead. A person of type C, for instance, might prefer for at least 50% of their neighbours to be of a type that isn't C. An example of this is shown in Simulation 2.
We find that not a whole lot has changed from before. The self-seeking groups (blue and pink) continue to agglomerate into localised clusters. The newly added diversity-seeking group (orange) mostly gathers around the edges of these neighbourhoods and occasionally manages to infiltrate them.
Gnillehcs' Model of Integration
In the final experiment, Simulation 3, we see what happens when each groups' preference changes over time.
We do this by linearly decreasing Group 1, 2, and 3's similarity threshold from from a preference for similarity (~60%) to a preference for diversity (~-40%) throughout the course of the simulation. This represents groups that are gradually shifting their preference from similarity towards diversity.
To make things interesting, for Group 4, we start from a point of indifference (0%) and linearly increase their threshold to a strong preference for similarity (77%).
In the first part of the simulation, when all four groups prefer similarity, we see the classic Schelling segregation behaviour. However, once the households have self-organised into highly homogenous clusters, even the slightest preference for diversity sparks an exodus. Even the self-seeking Group 4 is gradually dispersed as its clusters become overwhelmed by the other groups.
It turns out Schelling's original observation about mild preferences works both ways: highly segregated neighbourhoods readily disintegrate in the presence of a slight preference for diversity.




Member discussion